Bezier Curve

베지어 곡선이란?

WIKIPEDIA 베지에 곡선

베지에 곡선은 컴퓨터 그래픽 및 관련 분야에서 사용되는 매개변수 곡선입니다. 일련의 ‘제어점’은 공식을 통해 부드럽고 연속적인 곡선을 정의합니다.

3차 Bezier 곡선을 위해서는 네 개의 점이 필요하다.

\[\mathbf{P}_0, \mathbf{P}_1, \mathbf{P}_2, \mathbf{P}_3\]

4개의 제어점을 이용해 다음과 같이 정의한다(Berstein 다항식):

\[ \mathbf{B}(t) = (1 - t)^3 \mathbf{P}_0 + 3t(1 - t)^2 \mathbf{P}_1 + 3t^2(1 - t) \mathbf{P}_2 + t^3 \mathbf{P}_3, \quad t \in [0, 1] \]

위 공식은 t값의 변화에 따라 점이 갖는 가중치를 반환한다. 예를 들어 시작점에서 vertex가 시작된다고 하면, 이 때 시작점의 가중치는 1.0이다. 그러나 vertex가 끝점으로 향하면 점차 시작점의 가중치는 0.0으로 줄어든다.

따라서 네 개의 점으로 다음과 같이 곡선을 표현할 수 있다.

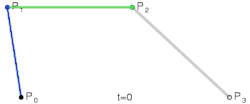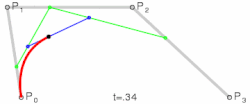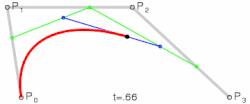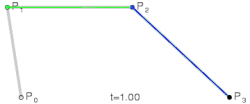
(이미지 출처: WIKIPEDIA)

3차뿐만 아니라 점의 개수를 늘려서 4차, 5차 곡선으로도 사용할 수 있지만, 3차 베지어 곡선을 많이 쓰는 이유는 4개의 제어점으로 충분히 다양한 곡선을 표현할 수 있기 때문이다.

3차 Bezier 곡선을 위한 Berstein 다항식:

public Vector4 BernsteinBasis(float t)
{
    float invT = 1.0f - t;
    
    return new Vector4(
        invT * invT * invT,
        3.0f * t * invT * invT,
        3.0f * t * t * invT,
        t * t * t);
}

각 점들에 대한 가중치를 계산한 좌표 반환 함수:

public static Vector3 Evaluate(Vector3[] controlPoints, float t)
{
    Vector4 basis = BernsteinBasis(t);
    return basis.x * controlPoints[0] +
            basis.y * controlPoints[1] +
            basis.z * controlPoints[2] +
            basis.w * controlPoints[3];
}

‘t’값에 따라 각 제어점에 곱해지는 가중치가 달라지며, 이를 통해 곡선은 시작점에서 끝점까지 부드럽게 이동하게 된다. 해당 곡선을 그리기 위한 좌표를 반환하는 것이다.

정점 4개를 사용해서 곡선 그리기:

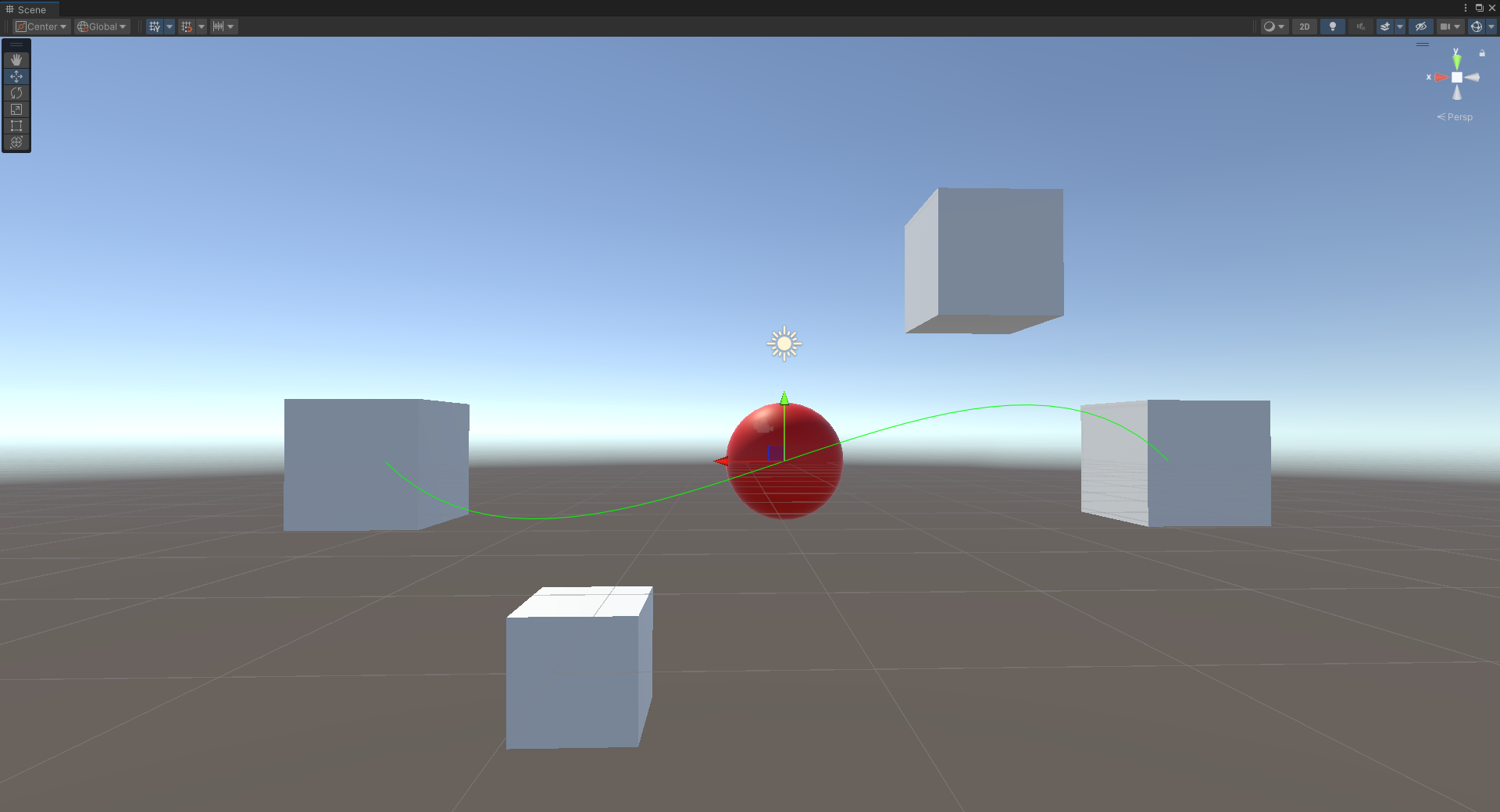
위 사진은 흰 색 Cube가 곡선을 결정하는 Vertex이다. 빨간 공이 t 값이 0 ~ 1로 변화하면서 빨간 공의 궤적이 곡선을 그리게 되는 것이다.

Bezier Surface는 Bezier Curve를 u방향과 v방향으로 각각 확장한 개념이다. 따라서 곡면을 시각적을 보면 여러 개의 곡선이 연결된 것처럼 보인다.

곡면을 위한 계산 함수:

public static Vector3 Evaluate(Vector3[] patch, float u, float v)
{
    Vector4 Bu = BezierCurve.BernsteinBasis(u);
    Vector4 Bv = BezierCurve.BernsteinBasis(v);
    return Sum(patch, Bu, Bv);
}

계산된 값을 합하는 함수:

private static Vector3 Sum(Vector3[] patch, Vector4 u, Vector4 v)
{
    Vector3 sum = Vector3.zero;
    for (int i = 0; i < 4; i++)
    {
        Vector3 temp = Vector3.zero;
        for (int j = 0; j < 4; j++)
        {
            temp += u[j] * patch[i * 4 + j];
        }
        sum += v[i] * temp;
    }
    return sum;
}

위에서 곡면에 t값에 따른 대한 u, v 값을 계산했다면 그 가중치에 맞게 합한다.

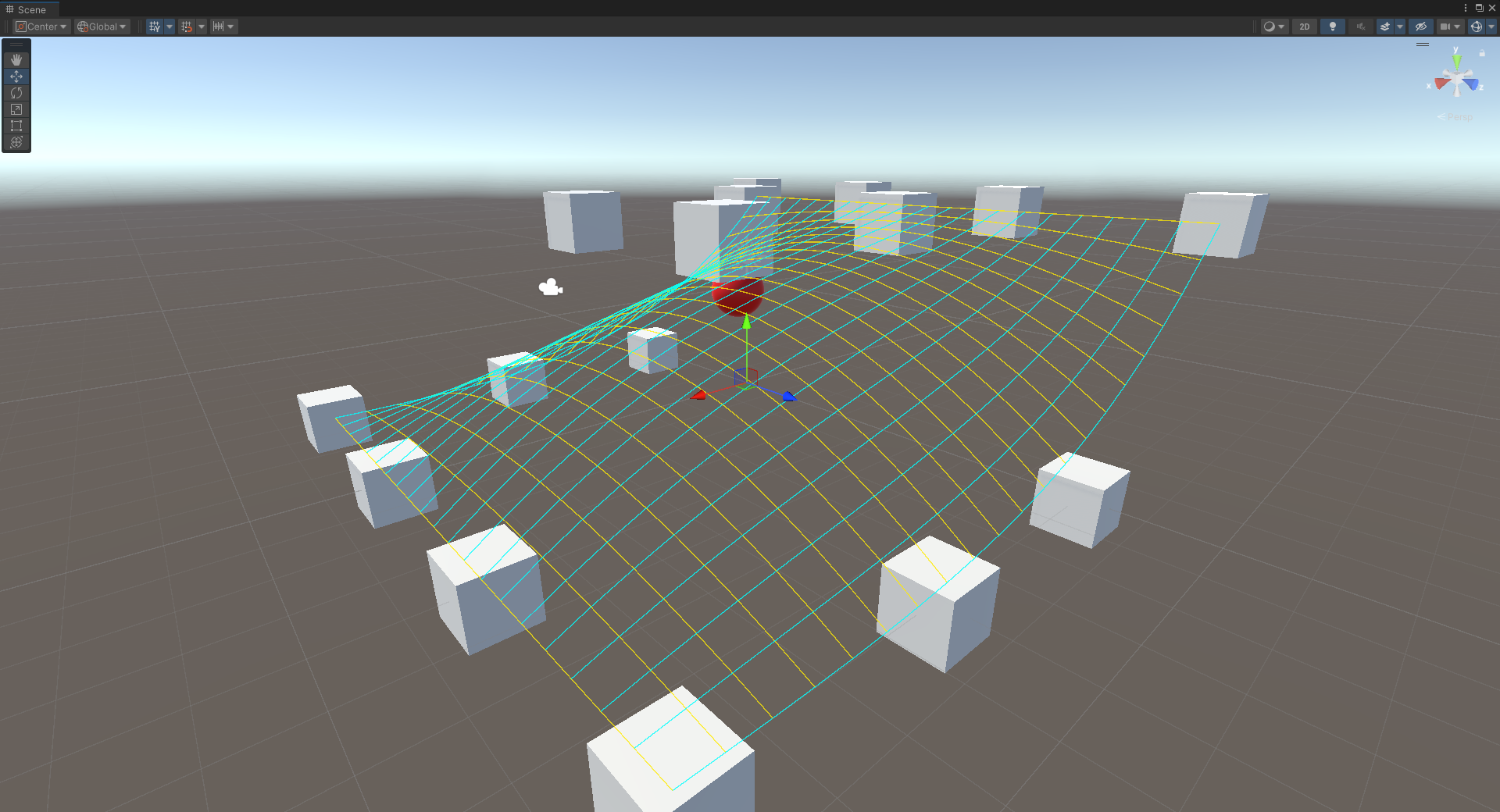
위 그림은 여러 개의 Bezier Curve가 격자 형태로 연결되어 하나의 Bezier Surface를 이루는 모습을 보여준다.

유니티 프로젝트는 여기에서 확인할 수 있습니다.